球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋
円錐台の体積を求める公式はあるようですが、 楕円錐台の体積を求める公式というのはあるのでしょうか? また仮に、上面と下面の楕円の面積がわかっているとすれば、 その公式はどのようになりますでしょうか?底面積がS,高さがh の円錐の体積は 1 3 Sh 半径r の球の体積は 4 3 ˇr3 であることを学んだ。しかし,中学校の教科書には,これらの事実の証明は書かれ ていない。以下では,円柱の体積の公式と高校の「数学B」までの知識を使って, 円錐の体積の公式を
円錐の体積 公式
円錐の体積 公式- スーちゃん 円すいの体積は円柱の3分の1ってならったよ森羅万象博士 三角すいや四角すいも3分の1になるね。なんでだろう。スーちゃん えっ錐体の体積の場合は、b=0で、c=a/4 (2乗に比例する)だから、 そうすると、4次元錐体の体積は、b=0で、c=a/8 (3乗に比例する)だから、 となるはず。 s:へー。あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。
円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明
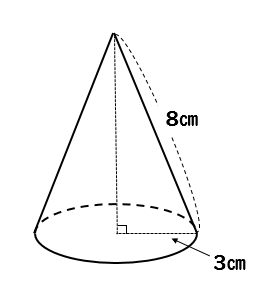
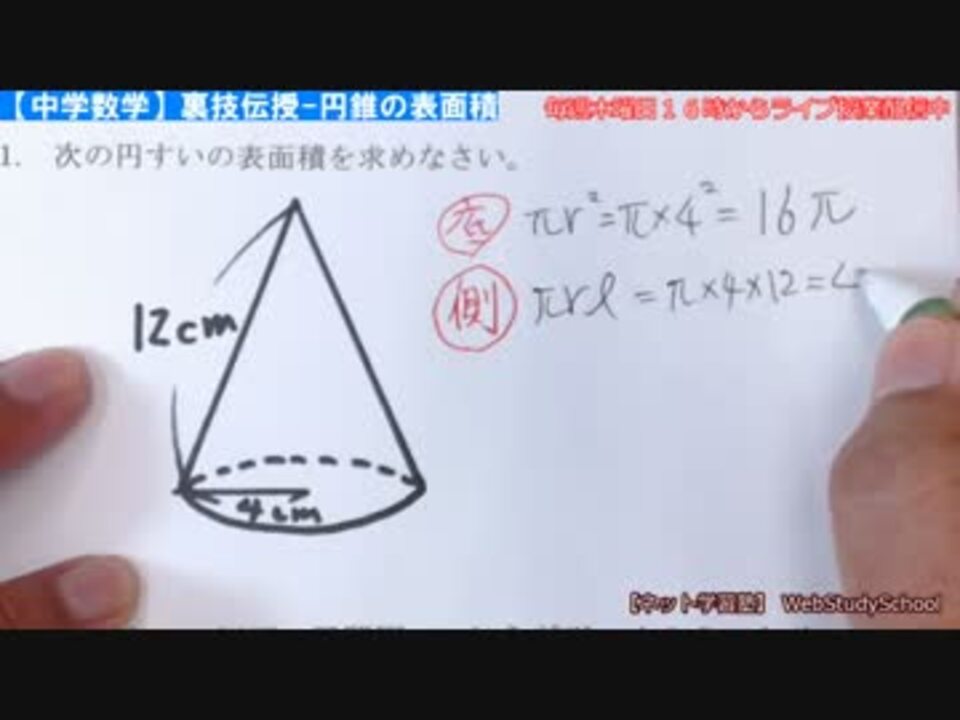
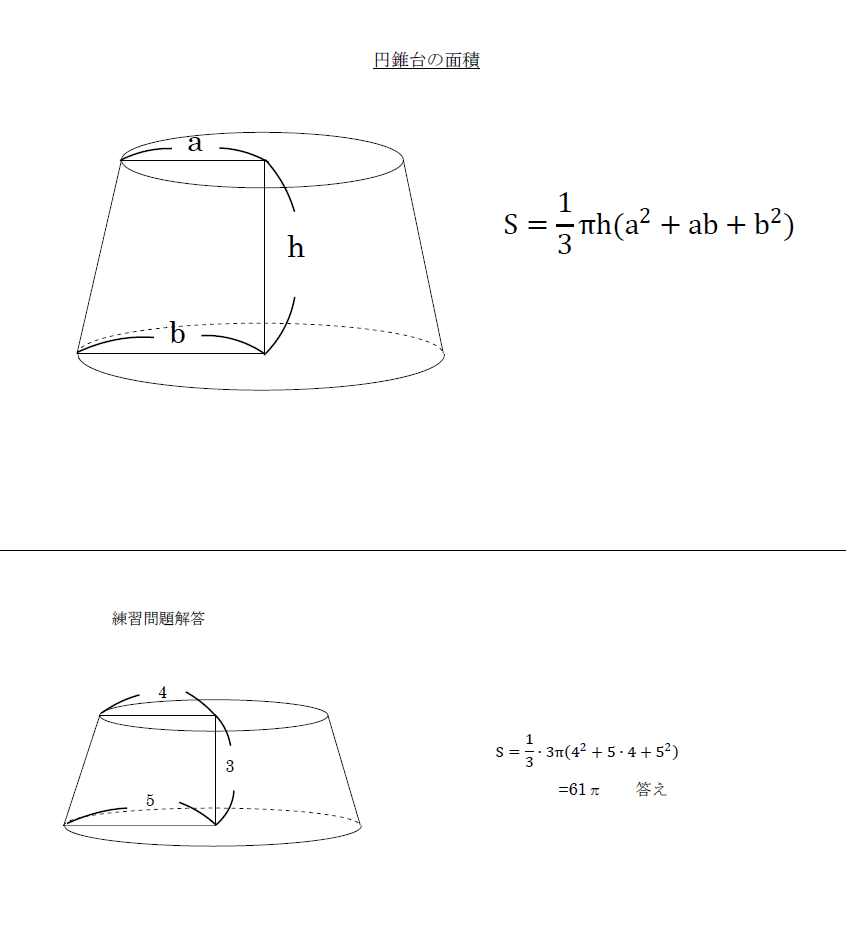
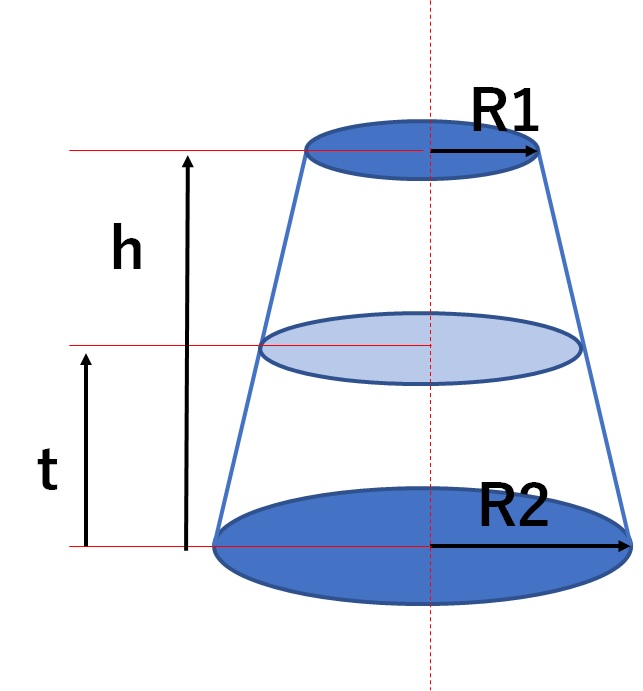
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S手っ取り早く円錐の体積を求めるには、この公式に値を代入すればよいだけです。 このページの続きでは、 公式の導出方法 も説明していますが、 公式を使わずに、順番に計算する方法 もお示ししますので、みなさんの必要に応じて使い分けてください。 計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく 円錐の表面積 12M views Discover short videos related to 円錐の表面積 on TikTok Watch popular content from the following creators 数スタ(@studyline3), 楽しく勉強あきとんとん(@akitonton), あ(@jpjpwagp), かずおっち(@kazuocci), Tonomura塾長
楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。 球 最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。球の体積、表面積 半径rの球 表面積=4πr 2 、 体積= 4 3 πr 3 r (例)半径6cmの円 6cm 表面積=4π×6×6=144π(cm 2) 体積= 4 3 π×6×6×6=2π(cm 3) 回転体の体積 回転体は、円錐や円柱、球などの組み合わせでできているので、 それぞれの部分で体積を出して足したり、引い
円錐の体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
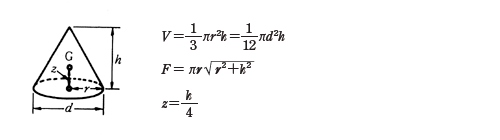 |  | |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 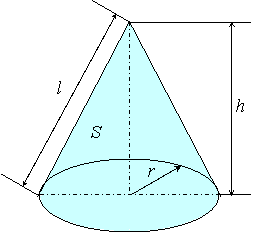 |
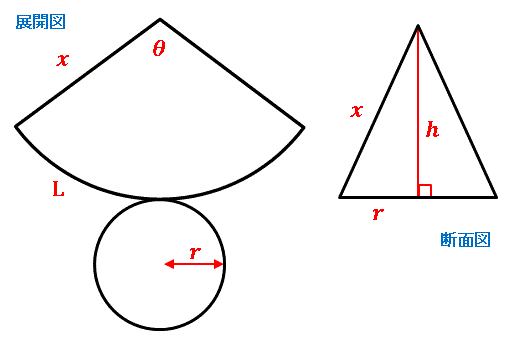
まとめ 円錐の高さを求める問題は、ほぼこの2パターン! 母線と半径から、三平方の定理を使って求める 体積と半径から、円錐の体積の公式を使って求める はかせちゃん 今日もお疲れ様でした~ また会える日を楽しみにしていますね 関連記事は 円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です
Incoming Term: 円錐の体積 公式, 円錐の体積 公式 証明, 円錐の体積 公式 覚え方,




0 件のコメント:
コメントを投稿